Journal number 2 ∘ Givi Lemonjava ∘
Capital Budgeting in Financial Modeling

journal N2 2025 

DOI: 10.52340/ekonomisti.2025.02.03

Annotation:The paper discusses the company's financial budgeting process and methods for evaluating investment projects. The paper provides an analysis of their strengths and weaknesses and identifies ways to overcome these weaknesses. The paper also develops an investment project evaluation model and a computer program for  use this model in practice. This tool was used to perform sensitivity analysis and show results of analysis graphically.

Keywords: Capital budgeting, Payback Period, Net Present Value (NPV), Internal Rate of Return (IRRI), Modified Internal Rate of Return, Profitability Index (PI), and Hurdle Rate of Return.

Introduction

Capital budgeting is one of the pivotal tools that evaluate the returns expected from investments projects[1,2]. Using these tools, a company assesses the risks and returns properly and make informed decisions to achieve its objectives. The most firms employ several types of capital – capital components: debt, preferred stock, and common stock. In this case, cost of capital should be weighted average cost of capital, or shortly – WACC, which is one of the most important components of the capital budgeting model, and the calculation of which is based on the weights determined by the target capital structure of the company[6].

The target capital structure describes the mix of debt, preferred stock, and common equity expected to optimize a company’s price. As a company raises new capital, it will focus on maintaining this target or optimal capital structure - the perfect balance between maximising the wealth and worth of the company and minimising its cost of capital. Due to debt cost tax deductibility, debt financing offers the lowest cost of capital. However, too much debt increases the financial risk to shareholders and the return on equity that they require. Because of that, companies are trying to have the optimal point at which the marginal benefit of debt equals the marginal cost. Capital budgeting decisions include: 1) decisions on a product, service, facility, or activity; 2) sound estimates of the timing and amount of cash flow for the proposal; 3) a predetermined criterion for making or rejecting a decision.

Companies with consistent, stable cash flows can tolerate a much larger debt load and will have a much higher percentage of debt in their optimal capital structure. Conversely, a company with volatile cash flows will have little debt and a large amount of equity. It is difficult to pinpoint the optimal capital structure; therefore, managers have to make decisions within a certain range[6,7]. The task of selecting the optimal capital structure is also complicated by the fact that a healthy blend of debt and equity varies according to the industries involved, line of business, and a firm's stage of development, and can also vary over time due to external changes in interest rates and regulatory environment.

There are two types of factors effected on cost of capital. One is that which the firm can control, and another – cannot. Capital structure policy, dividend policy and investment policy are instruments effecting on capital cost, and the interest rate, market risk premium and tax rates are outside internal control. The company's goal should be to be as close as possible to the optimal capital budget point, where marginal cost of capital (MCC) equals the incremental expected return. The Figure 1 shows the marginal cost of capital and investment opportunity schedule.

The MCC of a company tends to increase as it raises additional capital. As the company makes additional investments with this new capital, returns on its investments will generally decrease as represented by the investment opportunity schedule (IOS). The relationship between the MCC and the IOS gives an overview of the basic decision-making problem that a company has.

Businesses could pursue projects and opportunities that might enhance shareholder value and profit. Because  business has available the amount of capital for new projects is limited, management intensively  uses capital budgeting techniques.

 

Figure 1

There  are a number of capital budgeting methods. Among  them, the most commonly used are: payback period,  discounted payback period,  net present value (NPV), internal rate of return (IRR), modified internal rate of return (MIRR), and  profitability index[3].    

Payback Period

The payback period is a financial analytical tool that defines the length of time necessary to earn back money that has been invested. Calculating the payback period can give an investor some insight into the degree of riskiness that the investment represents.

The payback periods of two investment projects are outlined in Table 1.

 

Each project requires an initial $1,000 investment. But each project varies in payback periods and number of cash flows generated. Which project is the best? Project (A) and (B) have consistently 4 and 3.33 years, but project (A) generates $500 more cash than project (B). The Payback Period method is most useful for comparing projects with nearly equal lives, or for companies that focus on smaller investments, mainly because smaller investments usually don’t involve overly complex calculations.

The payback period shows us how long it takes for the return on investment, but it does not show what is the amount of investment’s return, and: it doesn’t accounting for the time value of money, risk factors, financing concerns or the opportunity cost of an investment.  For this reason, payback periods calculated for longer-term investments have a greater potential for inaccuracy. Therefore, using the payback period in combination with other capital budgeting methods is far more reliable.

Discounted Payback Period

The discounted payback period is a modified version of the payback period. It is similar to the regular payback period except that the expected cash flows are discounted and take account for the time value of money. In this metric, future cash flows are estimated and adjusted for the project’s cost of capital.

There are two steps involved in calculating the discounted payback period. First, we must discount  the net cash flows that will occur during each year of the project; and, second, to obtain the discounted payback period, we must subtract the discounted cash flows from the initial cost figure - this continues until the initial cost figure becomes zero.

Table 2 shows one example of discount payback period calculation.

 

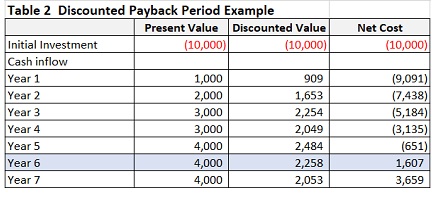
In this case, the project’s payback period is 5.16 years (5+ 651/4000= 5 + 0.16 = 5.16). 

One common disadvantage of both the payback period and discounted payback methods is that it that they ignore the cash flows after the payback period which are serious deficiencies. 

Net Present Value (NPV)

Net present value takes into consideration all the inflows, outflows, period of time, and risk involved.This method compares the present value of a project’s cash inflow to the present value of its outflows. Discounting the after-tax cash flows by the weighted average cost of capital or hurdle rate of return allows us to determine whether a project will be profitable or not. It also determines how profitable a project will be in comparison with alternatives. In common, Positive NPV should results in positive economic value added (EVA) and positive market value added (MVA).

According to NPV rule: all projects with a positive net present value should be accepted, and those that are negative should be rejected. A positive (negative) net present value means that the rate of return on the capital investment is greater (less) than the discount rate used in the analysis.  In the case when funds are limited, only projects with the highest discounted value should be accepted.

In the case of incompatible projects, as shown in Fig. 2, if the cost of capital is less than 6%, NPV_A exceeds NPV_B and project A will be chosen, and if it is higher than 6%, then project B will be chosen.

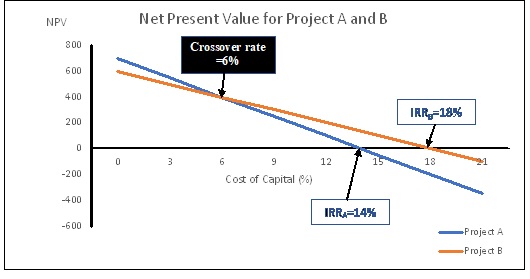
Figure 2

The NPV outcome heavily depend on inputs, estimates, and long-term projections of cash flows. Among them is discount rate which reflects the opportunity cost of capital and the associated with the investment. The weighted average cost of capital (WACC), industry benchmarks, or the required rate of return for similar investments can be considered as a discount rate. A higher discount rate will reduce the present value of future cash flows, potentially leading to a lower NPV, while a lower discount rate will have the opposite effect. Therefore, careful consideration should be given to the selection of the discount rate based on the specific context of the investment.

NPV is important metrics of an investment project as it gives money measure of benefit of the project to shareholders. NPV can be used to compare a projected rate of return with the hurdle rate required to approve an investment. The discount rate in the NPV formula is a hurdle rate for a project based on a company’s cost of capital, such as the weighted average cost of capital (WACC), and a negative NPV shows that the expected rate of return will fall short of it, meaning that the project will not create value.

Considering the fact that many businesses have a fixed budget and sometimes have two or more project options, NPV cannot be used for comparing the projects different in period of time; it doesn’t consider project size or return on investment (ROI[1]). It also relies heavily on inputs, estimates, and long-term projections,  which can have a significant impact on the outcome of a particular project’s valuation.

Internal Rate of Return (IRR)

The Internal Rate of Return (IRR) is the discount rate that makes the net present value (NPV) of a project zero.  The IRR formula is as follows: 

 

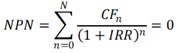
Unlike net present value, the internal rate of return doesn’t give you the return on the initial investment in terms of real dollars. Using IRR exclusively can lead you to make poor investment decisions, especially if comparing two projects with different durations.

According with NPV, proposed projects are usually accepted if they have a net positive value. In contrast, IRR is often accepted if the resulting IRR has a higher value compared to the existing cutoff rate or hurdle rate. Projects with a positive net present value also show a higher internal rate of return greater than the base value.

Let’s consider a company which hurdle rate is 12%, and one-year project A has an IRR of 25%, whereas five-year project B has an IRR of 15% (Table 3). If the decision is solely based on IRR, this will lead to unwisely choosing project A over B, while its NPV is 3.5 times higher than project A's NPV. 

 

Let's look at Fig. 1 again. If the cost of capital exceeds 6%, both methods will favor project B. A conflicting situation will arise if the cost of capital is less than 6%, because in this case, the NPV choice favors project A, and with IRR, the choice will be project B, this is when net present value of project B is less than the net value of project A, which would not be correct.

Another reason why NPV and IRR give different results in comparing mutually exclusive projects is that the first one considers the cost of capital as the reinvestment rate, and the second one - the IRR rate, which is less realistic. Accordingly, the NPV method is more reliable than IRR.

Using IRR exclusively can lead an investor to make poor investment decisions, especially if comparing two projects with different durations. Another very important point about the internal rate of return is that it assumes all positive cash flows of a project will be reinvested at the same rate as the project instead of the company’s cost of capital. Therefore, the internal rate of return may not accurately reflect the profitability and cost of a project. In the case when the duration of the comparable projects is different, the use of IRR can lead to an incorrect decision, which is clearly seen from the projects considered in Table 3.

In short, if the projects are independent, then NPV and IRR give the same result, but if they are mutually exclusive projects and, moreover, they are characterized by different scales and schedules, then NPV should be used as project choose criteria.

The Modified Internal Rate of Return (MIRR)

As we mentioned above, IRR assumes that all cash flows received from an investment are reinvested at the same IRR rate.  The MIRR allows us to set a different reinvestment rate for cash flows received.  Additionally, MIRR arrives at a single solution for any series of cash flows, while IRR can have two solutions for a series of cash flows that alternate between negative and positive (nonmoral[2] cash flows), as it shown by Figure 3.

 

Figure 3

MIRR is defined as follows:

 

Where: FVCF – the future value of positive cash flows at the reinvestment rate; PVCF – the present value of negative cash flows at cost of capital.

Projects that’s MIRR are above the expected return will be recommended to undertake, conversely – rejected. In addition, the MIRR is commonly employed to compare several alternative projects that are mutually exclusive. In such a case, the project with the highest MIRR is the most attractive.

 

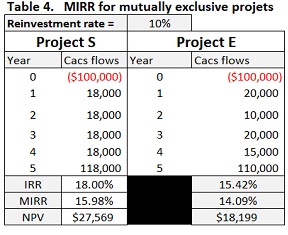
If the projects are of equal size and duration, then as shown in Table 4: 1) IRRS > IRRE, 2) MIRRS > MIRRE, and 3) NPVS > NPVE, and in other words, in this case, there is no conflict between the regular IRR, MIRR, and NPV.

Profitability Index

The Profitability Index (PI) measures the ratio between the present value of future cash flows and the initial investment. The index used for ranking investment projects and showing the value created per unit of investment. The profitability index considers the time value of money, allows companies to compare projects with different lifespans, and helps companies with capital constraints choose investments. It takes into consideration the time value of money and the risk of future cash flows through the cost of capital.

The formula for the PI is as follows:

 

To illustrate, let's consider an example. Suppose a company plans to invest one million dollars in (A)⋯(E) investment projects (Table 5), the total cost of which exceeds the amount allocated for investment.

 

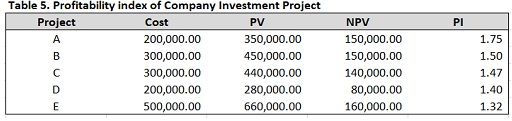
As can be seen from this table, the PI criterion requires the investment budget to select projects (A), (B), (C), and (D), whose total NPV is 520,000. The NPV criteria gives us following choice of projects: (A), (B), and (E). There NPV sum equals $460,000, which is worse than the previous choice made according criteria PI - $520,000. Although NPV is an important characteristic of an investment project taken separately, its use in this case, as we have seen, gives the wrong result.

The profitability index, using the cost of capital as discount rate considers the time value of money, allows companies to compare projects with different lifespans, and helps companies with capital constraints choose investments, which should result in the maximum increase in the value of the company.

MIRR has a significant advantage over the regular IRR. It assumes all reinvestments at the cost of capital, while IRR – at the own rate. Assumption - making reinvestment at cost of capital, is more correct and it gives better estimate of project’s profitability. If the mutually exclusive projects are equal size and have the same life spans, then NPV and MIRR will always lead to the same decision. The main advantage of NPV over MIRR/IRR is that it shows how much each project increases the value of the firm.

Hurdle Rate

A hurdle rate is the minimum rate of return required on an investment. Hurdle rates give companies clarity about whether they should pursue a specific project - the higher the risk, the higher the hurdle rate. The following factors should be considered when determining the hurdle rate: 1) risk premium, 2) inflation rate, 3) interest rate, 4) cost of capital, 5) and expected rate of return. It serves as a tool for align management decisions with the expectations of investors.

The hurdle rate differs from IRR. The hurdle rate is a minimum acceptable return on investment, while IRR is the rate at which all the net present value (NPV) of all cash flows from a project will be zero. If any project has an internal rate of return that exceeds its’ calculated required return, then it is accepted.

Most companies use their weighted average cost of capital (WACC) as a hurdle rate for investments. An alternative to making a new investment is buying back their own shares which would presumably earn their WACC as the rate of return. So, investing in their own shares (earning their WACC) represents the opportunity cost of any alternative investment.

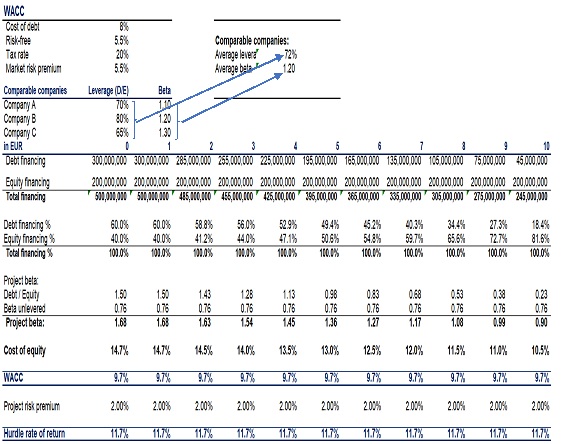
The WACC is calculated by weighing the cost of each capital component according to its proportion in the overall capital structure. If a company's WACC is 8% and the risk premium for a particular project is estimated at 4%, the hurdle rate for that project would be 12%.In practical terms, WACC is a benchmark that presents the minimum return a company must generate on its projects to satisfy its shareholders and debt holders. When a company evaluates new projects, using WACC plus the risk premium ensures that these initiatives are expected to yield returns at least equal to the company’s current cost of capital plus the risk premium. The complete algorithm for these calculations is shown in Table 11.

Another way of looking at the hurdle rate is that it’s the required rate of return investors demand from a company. Therefore, any project the company invests in must be equal to or ideally greater than its cost of capital. Riskier investments generally have greater hurdle rates than less risky ones, because more risk requires more risk premium.

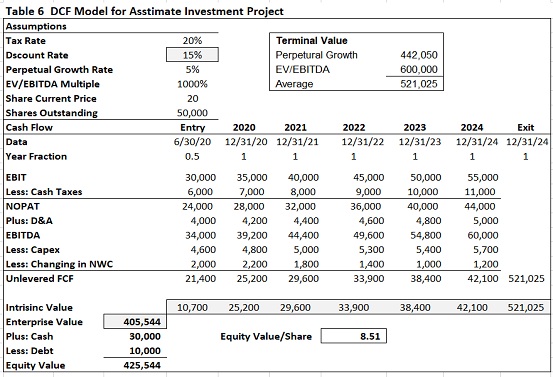
To  evaluate an investment  by performing a discounted cash flow (DCF) analysis we need to use  the hurdle rate.  The DCF analysis method uses the concept of the time value of money (opportunity cost) to forecast all future cash flows and then discount them back to today’s value to provide the net present value. Within framework of financial model using the hurdle rate in DCF analysis is illustrated in Table 6. This

As shown in this table, if a hurdle rate (discount rate) of 15% is used, the investment opportunity has a net present value of $405,544. This means if the cost of making the investment is less than $405,544, then its expected return will exceed the hurdle rate, and the project can be accepted. If the cost is more than $405,544, then the expected return will be lower than the hurdle rate, then the project will not be accepted.

 

Investment Project Estimate Excel Model (IPEEM)

Now, let’s Consider the model of project valuation called IPEEM[5]. This model is implemented in Visual Basic for Applications (VBA) for the windows operating system. This model allows us to calculate and list all above discussed all investment measures (Table 10).  

Model’s inputs of are listed in Figure 4. Based on this data, the model generates production accounts, profit and loss, balance sheet, and cash flow statements (Tables: 7, 8 and 9) [5]. The value stated here is not the current cash flows from business operations but they are incremental value expected from new investment projects. These increases are reduced by taxes, the rate of which is 20%; and the cost of funds - 8; cost of capital - 12%.

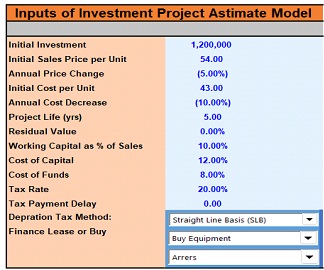
Figure 4

  

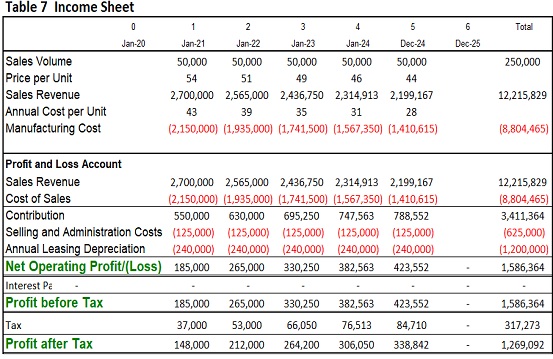
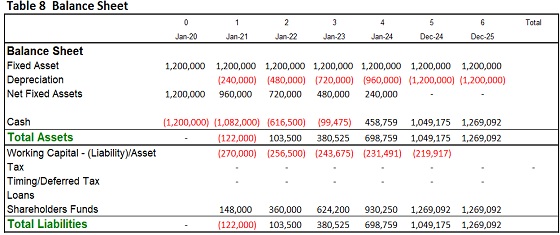
This model evaluates two options: buying or leasing the equipment. The estimates results based on the inputs given in Figure 1 are presented in Table 10.

 

As can be seen from this table, the internal rate of return of both projects, 23% and 17.2%, are sufficiently higher than the hurdle rate, which is 12%. But, buying a machine looks more preferable because of IRR_Buy is higher than IRR_Lease, NPV_Buy is higher than NPV_Lease, and the efficiency rate of buying is higher than the same characteristics of leasing. The advantage of leasing is indicated only by the accounting rate of return, 66.04% versus to 52.88%, but this is less indicative of the increase in the economic value of the company.

Another important component of the investment analysis and valuation model is sensitivity analysis, which allows us to visualize the impact on the investment outcome of changes in the essential variables that are included in the model parameters (Figure 5). In this case, these are the sales price, the price of funds, and the cost per unit of product. This analysis aims to estimate the effect of achieving project

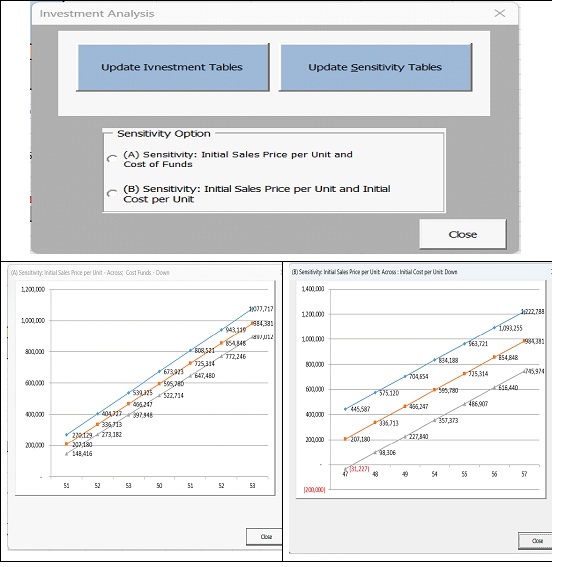
Figure 5

objectives if certain assumptions do not occur as projected. Sensitivity analysis is a technique that can show us the impact of changes in key project variables on the baseline project outcome. As can be seen from this figure 5, the value of the NPV of a given investment project strongly depends on the listed parameters of the model, which is noteworthy and should be taken into account when making a final  investment decision. The same analysis should be applied to the other measures discussed here, such as  IRR, MIRR, and PI.

Conclusion

As we have seen above, each of the capital budgeting methods discussed has advantages and disadvantages. The Payback Period is simple and shows the liquidity of the investment. But it doesn’t account for the time value of money or the value of cash flows received after the payback period. The Discounted Payback Period incorporates the time value of money but still doesn’t account for cash flows received after the payback period. NPV is important because it gives a direct measure of benefit of the project to interest-holders. A positive (negative) Net Present Value means that the rate of return on the capital investment is greater (less) than the discount rate used in the analysis.  In the case when funds are limited, only projects with the highest discounted value should be accepted and all positive NPV projects can't be initiated. So, we should look at NPV as the single best measure of profitability. As for IRR and MIRR, they also measure profitability, but in percentage terms, which many decision makers prefer. MIRR has an advantage over IRR because it takes into account that the reinvestment rate may not always be equal to the IRR of return. For decision makers, the profitability index (PI) is also quite informative and shows how much is expected to be received per unit of invested money which is valuable for comparing projects.   

If the projects are mutually independent, then the NPV, IRR, MIRR, and PI methods will have the same decision on whether to accept or reject the project.  If projects are mutually exclusive, then the ranking of projects can be conflicting, and to make the right decision, additional procedures will need to be implemented.

Which capital budgeting method should you use? There is no unequivocal answer. Each one has unique advantages and disadvantages, and some companies often use all of them. Currently, this is not so difficult to do with the help of modern computer technologies, which is clearly evidenced by Table 10, which is the result of the IPEEM software created for this purpose. This increases the quality of project evaluation and the awareness of the decision maker, because each one provides a different perspective on the capital investment decisions.

The result of the project evaluation depends on several key input parameters of the evaluation model. In our case, these were: 1) unit product price, 2) cost of funds, and 3) cost per unit product (see Figure 5).  As can be seen from figure 5, the result of the project evaluation is highly sensitive to the listed parameters of the estimated model, therefore, this issue should be properly taken into account in the assessment of the investment project’s value.

When the NPV of all existing investment projects is determined and the available amount of resources required for their implementation is also determined, it is possible to use the linear programming method and thus determine the optimal capital budget.

Table 11 An investment project’s the cost of capital and hurdle rate calculation model

 

 Literature

1. Ogden J.; Jen F. C.; Connor P. F. (2002) Advanced Corporate Finance. Practical Hall.

2. Ross; Westerfield; Jaffe (2002) Corporate Finance, 6^th Ed. McGraw-Hill.

3. Brigham, E. F. and Whrhardt, M. C. (2005) Financial Management, 11^th Ed, Thomson South-western.

4. Alastair L. Day (2005) Mastering Financial Modeling in Microsoft Excel, 2^th Ed, Practical Hall, Financial Times.

5. Lemonjava G.  (2024) Company Financial Modeling and Forecasting. Journal Ekonomist, 2, vol. XX  2024.

6. Hovakimian, A.; Hovakimian, G.; Tehranian, H. (2004) Determinants of target capital structure: The case of dual debt and equity issues. Journal of Financial Economics 71: 517-540.

7. Sibindi, A. (2016). Determinants of capital structure: A literature review. Risk governance & control: financial markets & institutions, 6(4-1), 227-237. https://doi.org/10.22495/rcgv6i4c1art13

---