
ივანე ჯავახიშვილის სახელობის თბილისის სახელმწიფო უნივერსიტეტის პაატა გუგუშვილის სახელობის ეკონომიკის ინსტიტუტის რეცენზირებადი, ბეჭდურ-ელექტრონული, საერთაშორისო სამეცნიერო-ანალიტიკური ჟურნალი

ეკონომიკის ბუნებრივი დონიდან გადახრის დამახასიათებელი ინვესტიციების მულტიპლიკატიური მოდელი და მისი ემპირიული რეალიზაცია საქართველოს მაგალითზე
რეზიუმე. სტატიაში განხილულია კობ-დუგლასის, ეკონომიკის ბუნებრივი დონისა და ინვესტიციების თეორიის გაერთიანებით მიღებული ქვეყნის ეკონომიკის ბუნებრივი დონიდან გადახრის დამახასიათებელი ინვესტიციების მულტიპლიკატიური მოდელი.ამასთან საქართველოს ეკონომიკის მაგალითზე ემპირიულად შემოწმებულია აღნიშნული მოდელის ვარგისიანობა და შეფასებულია მისი გამოყენების ვალიდურობა.სტატიაში წარმოდგენილია კობ-დუგლასის, ეკონომიკის ბუნებრივი დონისა და ინვესტიციების თეორიის სინთეზისგან მიღებული ინვესტიციების მოდელი. აღნიშნული ინვესტიციების მოდელის ემპირიული რეალიზაციით საქართველოს მაგალითზე დგინდება, რომ მოდელი სტატისტიკურად ვარგისია, მთლიანი ინვესტიციებისა და ძირითადი კაპიტალის წინა მნიშვნელობის თანაფარდობასთან ზრდად დამოკიდებულებაშია მშპ-ს მიმდინარე და წინა მნიშვნელობის თანაფრდობა, ხოლო კლებად დამოკიდებულებაშია დასაქმებულთა მიმდინარე პერიოდის თანაფარდობა მის წინა პერიოდის მნიშვნელობასთან. ამასთან, ასევე კლებად დამოკიდებულებაშია 2008 წლის აგვისტოს ომის ფაქტორი საშედეგო ცვლადთან, რაც ლოგიკური შედეგია.
საკვანძო სიტყვები: ეკონომიკის ბუნებრივი დონიდან გადახრის დამახასიათებელი ინვესტიციების მულტიპლიკატორული მოდელი, კობ-დუგლასიის საწარმოო ფუნქცია, ეკონომიკის ბუნებრივი დონე.
შესავალი
1928 წელს მათემატიკოსი ჩარლზ კობი და ეკონომისტი პოლ დუგლასი მივიდნენ დასკვნამდე, რომ ამერიკის შეერთებულ შტატებში 1899-1922 წლებში გამოშვებას, ფიზიკურ კაპიტალს და შრომას შორის დამოკიდებულებას კარგად ასახავდა საწარმოო ფუნქცია:
![]() (1)
(1)
სადაც Yt - გამოშვებაა t პერიოდში, Kt - ძირითადი კაპიტალის მოცულობა t პერიოდში, Lt - დასაქმებულთა რაოდენობა t პერიოდში. ამასთან α ნულსა და ერთს შორის მდებარეობს. დღესდღეისობით აღნიშნული ფუნქცია ცნობილია, როგორც კობ-დუგლასის საწარმოო ფუნქციის სახელით და კარგად ხსნის დამოკიდებულებას გამოშვებასა, კაპიტალს და შრომას შორის.
აღნიშნული ფუნქცია ეყრდნობა შემდეგ ორ დაშვებას: 1) მასშტაბის მუდმივი უკუგების; 2) კაპიტალის და შრომის კლებადი უკუგების შესახებ. თუ (1) მოდელში გავითვალისწინებთ ტექნოლოგიურ ფაქტორს, რომელიც ზემოქმედებას ახდენს როგორც კაპიტალის ასევე შრომის გამოყენების ეფექტიანობაზე მაშინ მივიღებთ:
![]() (2)
(2)
სადაც Tt - ტექნოლოგიური პროგრესის მაჩვენებელი ცვლადია t პერიოდში.
კობ-დუგლასის, ეკონომიკის ბუნებრივი დონისა და ინვესტიციების თეორიის გაერთიანებით მიიღება ქვეყნის ეკონომიკის ბუნებრივი დონიდან გადახრის დამახასიათებელი ინვესტიციების მოდელი.
ეკონომიკის ბუნებრივი დონიდან გადახრის დამახასიათებელი ინვესტიციების მულტიპლიკატიური
მოდელი და მისი ემპირიული რეალიზაცია
როდესაც ეკონომიკა იმყოფება ბუნებრივ დონეში, სადაც დასაქმებულთა და კაპიტალის რაოდენობა ოპტიმალურია შეიძლება ჩაიწეროს შემდეგი სახით:
![]() (3)
(3)
სადაც Y* - მშპ-ს ბუნებრივი მოცულობაა, Tt - ტექნოლოგიური პროგრესის მაჩვენებელი ცვლადი t პერიოდში, K* - ძირითადი კაპიტალის ბუნებრივი მოცულობა, L* - დასაქმებულთა ბუნებრივი რაოდენობა, τt - ფარდობითი ტექნოლოგიური პროგრესის ცვლადი.
მოდელი ეფუძნება დაშვებებს: 1) დროის ყოველ პერიოდში ეკონომიკა მიისწრაფის მის ბუნებრივ დონემდე; 2) დროის ყოველ ტაქტში ტექნოლოგიური ცვლილებების გამო იცვლება მშპ-ს ბუნებრივი დონე და იგი განისაზღვრება როგორც წინა დროითი ტაქტის ბუნებრივი დონის მოცულობის ნამრავლით მიმდინარე პერიოდის და წინა პერიოდის ტექნოლოგიური პროგრესის ცვლადების ფარდობაზე.
უკანასკნელი დაშვება შეიძლება ინტერპრეტირებულ იქნას შემდეგი სახით: დროის საწყის პერიოდში არსებული მშპ-ს ბუნებრივი დონე ყოველ პერიოდში განიცდის ცვლილებას და კორექტირდება ყოველი პერიოდის ტექნოლოგიური ცვლადით Tt. აღნიშნულის გათვალისწინებით ბუნებრივი მშპ-ს მიმდინარე მნიშვნელობა t პერიოდში შეიძლება წარმოდგინდეს მშპ-ს საწყისი ბუნებრივი დონით (Y*):
![]()
![]()
რეკურენტული ჩასმით და იმ ფაქტის გათვალისწინებით, რომ დროის პირველი ტაქტის მშპ-ს ბუნებრივი დონე წარმოადგენდა Y*-ს, ვღებულობთ:
![]() (4)
(4)
თუ შემოვიღებთ ტექნოლოგიური ცვლილების ფარდობით კოეფიციენტებს
![]() (5)
(5)
![]()
აღნიშნული კოეფიციენტი გამოსახავს ტექნოლოგიური პროგრესით გამოწვეულ მშპ-ს ბუნებრივი დონის ცვლილებას საწყის პერიოდთან მიმართებაში.
თუ გამოშვების ბუნებრივ და მიმდინარე დონეებს გავალოგარითმებთ და წრფივი სახით წარმოვადგენ მივიღებთ:
ბუნებრივი დონისთვის
![]() (6)
(6)
![]()
![]() (7)
(7)
![]()
მიმდინარე მნიშვნელობებისთვის
![]() (8)
(8)
![]()
(7) და (8) განტოლებებით შეგვიძლია ჩავწეროთ ბუნებრივი დონიდან მიმდინარე მშპ-ს მნიშვნელობის გადახრის განტოლებები:
![]() (9)
(9)
![]() (10)
(10)
გამარტივებით ვღებულობთ:
![]() (11)
(11)
![]() (12)
(12)
თუ (11) განტოლებას გამოვაკლებთ (12)-ს და დავაჯგუფებთ მივიღებთ:
![]() (13)
(13)
(13) მოდელიდან გამოვსახოთ ძირითადი კაპიტალის ლოგარითმული მნიშვნელობების სხვაობა.
![]() (14)
(14)
(14) მოდელში ინვესტიციების ცვლადის შეტანისთვის აუცილებელია მოდელი ძირითადი კაპიტალის ცვლადებს არ ჰქონდეთ ლოგარითმები, ვინაიდან IN=Kt+Kt-1. აღნიშნული პრობლემის დაძლევა შესაძლებელია (14) მოდელისთვის გამოვიყენოთ ტეილორის გაშლა.
ტეილორის თეორემა:
თუ ʄ ფუნქციას აქვს n+1 რიგამდე ჩათვლით წარმოებულები და a და x ჴის შემცველ ინტერვალზე, მაშინ ფუნქციის მნიშვნელობა x წერტილში მოიცემა ფორმულით:
![]() (15)
(15)
სადაც Rn ნაშთი განსაზღვრულია ტოლობით
![]() (16)
(16)
(15) ტოლობას ტეილორის ფორმულა ან ტეოლორის მწკრივი ეწოდება. თუ ნაშთს გამოვტოვებთ მაშინ (15)-ს ეწოდება ∫(x)-ის ტეილორის პოლინომური აპროქსიმაზია. აღნიშნული თეორიის მიხედვით ნებისმიერი გლუვი ფუნქცია შეიძლება მივაახლოვოთ მრავალწევრებით.
Rn ნაშთის წარმოსადგენად აგრეთვე იყენებენ ალტერნატიულ ფორმულას
![]()
აღნიშნულს ნაშთის ლაგრანჟის ფორმა ეწოდება.
ერთ ცვლადზე და წრფივი მიახლოებისას გამოიყენება (15) მოდელის მოდიფიცირებული ვარიანტი:
![]() (17)
(17)
(14) ჩაწერა (17) წრფივი აპროქსიმაციით Kt-1 -ზე მიიღება:
![]()
თუ აღნიშნულ ფორმულაში გავითვალისწინებთ წმინდა ინვესტიციების მნიშვნელობას IN = kt-Kt-1 მივიღებთ:
![]() (18)
(18)
მთლიან ინვესტიციებზე გადასასვლელად აუცილებელია გავითვალისწინოთ ძირითადი კაპიტალის ცვეთა.
![]() (19)
(19)
თუ (19) მოდელის ორივე მხარეს გავყოფთ Kt-1-ზე მივიღებთ:
![]() (20)
(20)
აღნიშნული მოდელის შესაფასებლად საქართველოს ეკონომიკის მაგალითზე (20) მოდელში უნდა ჩავრთოთ შემთხვევითი წევრი, 2008 წლის აგვისტოს ომის შედეგების გამომსახველი ცვლადი.
![]() (21)
(21)
ამასთან, საქართველოს ეკონომიკის მაგალითზე არ გაგვაჩნია ემპირიული ინფორმაცია ტექნოლოგიური პროგრესის შესახებ და როგორც ინვესტიციების აქსელერატორის მოდელის ემპირიულ რეალიზაციის დროს აღინიშნა ჴ ძირითადი კაპიტალის ცვეთის ნორმის შესახებ [8, მიქელაძე, გვ. 154-164].
თუ ძირითადი კაპიტალის ცვეთის ნორმის შესახებ გავაკეთებთ დაშვებას მისი დროში მუდმივობის შესახებ, მაშინ მისი მნიშვნელობის დასადგენად და მოდელში გასათვალისწინებლად შეიძლება გამოვიყენოთ 2 მიდგომა:
- ძირითადი კაპიტალის ცვეთის ნორმის მნიშვნელობა გამოთვლილია ინვესტიციების აქსელერატორის მოდელის შეფასებისას და აღნიშნული მნიშვნელობა გავითვალისწონოთ (21) მოდელის შეფასებისას.
- (21) მოდელის შეფასებისას შევაფასოთ კაპიტალის ცვეთის ნორმა, როგორც თავისუფალი წევრი. ვინაიდან მოდელი არ შეიცავს თავისუფალ წევრს და შეფასებისას არ წარმოგვექმნება პრობლემა თუ რა ნაწილს წარმოადგენს შეფასებულ კოეფიციენტის მნიშვნელობაში იგი.
(21) მოდელის შეფასების წინ გამოვიყენოთ ლოგარითმის თვისება ერთფუძიანი ლოგარითმების სხვაობის შესახებ და გარდავქმნათ იგი როგორც:
![]() (22)
(22)
(22) მოდელის შეფასებისას სასურველია შედეგობრივი ცვლადიც გავალოგარითმოთ, რაც პრაქტიკული თვალსაზრისით გულისხმობს რომ გადავალთ ცვლადებს შორის ზრდის ტემპების კავშირზე.
![]() (23)
(23)
ვინაიდან არ გვაქვს ინფორმაცია ტექნოლოგიური პროგრესის ცვლადის შესახებ მოდელი შევამოწმოთ აღნიშნული ცვლადის გამოტოვებით, აღნიშნული ქმედება ასახვას ჰპოვებს დეტერმინაციის კოეფიციენტებში. საშედეგო ცვლადის ემპირიული მნიშვნელობების დასადგენად, კერძოდ ძირითადი კაპიტალის მნიშვნელობებად გამოვიყენებთ ინვესტიციების აქსელერატორის მოდელის მიხედვით გამოთვლილ კაპიტალის კვარტალური მნიშვნელობებს. შევამოწმოთ დროითი მწკრივები სტაციონალურობაზე დიკი - ფულერის ტესტით [17, Dickey..., P.427-431].
ცხრილი1: დროითი მწკრივების შემოწმება სტაციონალურობაზე დიკი-ფულერის ტესტით
|
Null Hypothesis: LN_I_K has a unit root |
|
|||
|
Exogenous: None |
|
|
||
|
Lag Length: 4 (Automatic - based on SIC, maxlag=10) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t-Statistic |
Prob.* |
|
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller test statistic |
-0.396355 |
0.5364 |
||
|
Test critical values: |
1% level |
|
-2.608490 |
|
|
|
5% level |
|
-1.946996 |
|
|
|
10% level |
|
-1.612934 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
*MacKinnon (1996) one-sided p-values. |
|
|||
|
Null Hypothesis: LN_I_K has a unit root |
|
|||
|
Exogenous: Constant, Linear Trend |
|
|||
|
Lag Length: 4 (Automatic - based on SIC, maxlag=10) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t-Statistic |
Prob.* |
|
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller test statistic |
-2.028837 |
0.5726 |
||
|
Test critical values: |
1% level |
|
-4.137279 |
|
|
|
5% level |
|
-3.495295 |
|
|
|
10% level |
|
-3.176618 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
*MacKinnon (1996) one-sided p-values. |
|
|||
|
Null Hypothesis: LN_I_K has a unit root |
|
|||
|
Exogenous: Constant |
|
|
||
|
Lag Length: 4 (Automatic - based on SIC, maxlag=10) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t-Statistic |
Prob.* |
|
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller test statistic |
-2.081438 |
0.2528 |
||
|
Test critical values: |
1% level |
|
-3.557472 |
|
|
|
5% level |
|
-2.916566 |
|
|
|
10% level |
|
-2.596116 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
*MacKinnon (1996) one-sided p-values. |
|
|||
|
|
|
|
|
|
|
Null Hypothesis: D(LN_I_K) has a unit root |
|
|||
|
Exogenous: None |
|
|
||
|
Lag Length: 3 (Automatic - based on SIC, maxlag=10) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t-Statistic |
Prob.* |
|
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller test statistic |
-3.707682 |
0.0004 |
||
|
Test critical values: |
1% level |
|
-2.608490 |
|
|
|
5% level |
|
-1.946996 |
|
|
|
10% level |
|
-1.612934 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
*MacKinnon (1996) one-sided p-values. |
|
|||
როგორც ვხედავთ ![]() წარმოდგენს პირველი რიგის ინტეგრირებად პროცესს, ვინაიდან მიიღება დიკი-ფულერის ტესტის ალტერნატიული ჰიპოთეზა ერთეულოვანი ფესვის არსებობაზე [17, Dickey..., P.427-431].
წარმოდგენს პირველი რიგის ინტეგრირებად პროცესს, ვინაიდან მიიღება დიკი-ფულერის ტესტის ალტერნატიული ჰიპოთეზა ერთეულოვანი ფესვის არსებობაზე [17, Dickey..., P.427-431].
ცხრილი2: ინვესტიციებისა და ძირითადი კაპიტალის ფარდობის ლოგარითმული მნიშვნელობის შემოწმება სტაციონალურობაზე დიკი-ფულერის ტესტით
|
Null Hypothesis: LN_GDP_F has a unit root |
|
|||
|
Exogenous: None |
|
|
||
|
Lag Length: 3 (Automatic - based on SIC, maxlag=10) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t-Statistic |
Prob.* |
|
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller test statistic |
-1.788027 |
0.0703 |
||
|
Test critical values: |
1% level |
|
-2.607686 |
|
|
|
5% level |
|
-1.946878 |
|
|
|
10% level |
|
-1.612999 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
*MacKinnon (1996) one-sided p-values. |
|
|||
დიკი-ფულერის ტესტით ![]() მწკრივის სტაციონალურობაზე შემოწმებისას მიიღება ნულოვანი ჰიპოთეზა 10%-იანი მნიშვნელოვნების დონით მწკრივის სტაციონალურობის შესახებ [17, Dickey..., P.427-431].
მწკრივის სტაციონალურობაზე შემოწმებისას მიიღება ნულოვანი ჰიპოთეზა 10%-იანი მნიშვნელოვნების დონით მწკრივის სტაციონალურობის შესახებ [17, Dickey..., P.427-431].
ცხრილი3: მშპ-ს მიმდინარე და ლაგირებული მნიშვნელობის ფარდობის ლოგარითმული მნიშვნელობის შემოწმება სტაციონალურობაზე დიკი-ფულერის ტესტით
|
Null Hypothesis: LN_LP_F has a unit root |
|
|||
|
Exogenous: None |
|
|
||
|
Lag Length: 1 (Automatic - based on SIC, maxlag=9) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t-Statistic |
Prob.* |
|
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller test statistic |
-11.96170 |
0.0000 |
||
|
Test critical values: |
1% level |
|
-2.622585 |
|
|
|
5% level |
|
-1.949097 |
|
|
|
10% level |
|
-1.611824 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
*MacKinnon (1996) one-sided p-values. |
|
|||
ასევე სტაციონალურ მწკრივს წარმოადგენს ![]()
ომის ფაქტორი წარმოადგენს ფიქტიურ ცვლადს და მისი მნიშვნელობები გარდა 2009 წლის პირველი კვარტალისა, სადაც იგი 1-ის ტოლია, სხვა კვარტალებში მისი მნიშვნელობა 0-ს უტოლდება.
თუ ცვეთის ნორმის შესახებ გამოვიყენებთ მეორე მიდგომას და (23) მოდელს ისე შევაფასებთ მივიღებთ:
ცხრილი4: ცვეთის ნორმის მეორე მიდგომის შემთხვევაში (23) მოდელის შეფასებები უმცირეს კვადრატთა მეთოდის გამოყენებით
|
Dependent Variable: D_LN_I_K_F |
|
|||
|
Method: Least Squares |
|
|
||
|
Date: 06/09/18 Time: 14:17 |
|
|
||
|
Sample (adjusted): 2003Q3 2016Q4 |
|
|||
|
Included observations: 45 after adjustments |
|
|||
|
Convergence achieved after 1 iteration |
|
|||
|
D_LN_I_K_F=1/C(1)* LN_GDP_F+(1-C(1))/C(1)*LN_LP_F+C(3)+C(2)*WAR |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
|
|
|
|
|
|
|
|
|
|
|
|
C(1) |
0.550312 |
0.047829 |
11.50581 |
0.0000 |
|
C(3) |
0.001716 |
0.029127 |
0.058900 |
0.9533 |
|
C(2) |
-0.958743 |
0.199292 |
-4.810744 |
0.0000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
R-squared |
0.810887 |
Mean dependent var |
0.019193 |
|
|
Adjusted R-squared |
0.801881 |
S.D. dependent var |
0.427858 |
|
|
S.E. of regression |
0.190442 |
Akaike info criterion |
-0.414601 |
|
|
Sum squared resid |
1.523258 |
Schwarz criterion |
-0.294156 |
|
|
Log likelihood |
12.32851 |
Hannan-Quinn criter. |
-0.369700 |
|
|
F-statistic |
90.04460 |
Durbin-Watson stat |
2.290399 |
|
|
Prob(F-statistic) |
0.000000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ემპირიული მოდელი სტატისტიკურად ვარგისს წარმოადგენს და ამასთან დეტერმინაციის და კორექტირებული დეტერმინაციიის კოეფიციენტების მნიშვნელობებიც საკმაოდ მაღალია (0.81; 0.8)
ამასთან მოდელის ნარჩენობითი წევრები ნორმალურად არის განაწილებული.
გრაფიკი1: ცვეთის ნორმის მეორე მიდგომის შემთხვევაში (23) მოდელის ნარჩენობითი წევრების განაწილების ჰისტოგრამა
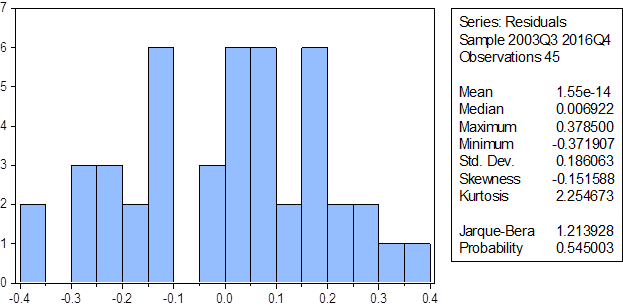
ბროიშ-გოდფრის ტესტის მიხედვით ნარჩენობით წევრებში შეინიშნება სერიული კორელაცია, ვინაიდან მიიღება ერთეულოვანი ჰიპოთეზა ავტოკორელაციის არსებობის შესახებ [16, Breusch, P., 334-355; 22, Godfrey, P. 1293-1301].
ცხრილი5: ცვეთის ნორმის მეორე მიდგომის შემთხვევაში (23) მოდელის ნარჩენობით წევრებში ავტოკორელაციის არსებობის შემოწმება ბროიშ-გოდფრის ტესტის მიხედვით
|
Breusch-Godfrey Serial Correlation LM Test: |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
F-statistic |
4.431168 |
Prob. F(2,40) |
0.0183 |
|
|
Obs*R-squared |
8.161811 |
Prob. Chi-Square(2) |
0.0169 |
|
|
|
|
|
|
|
|
|
|
|
|
|
ასევე აღნიშნული ემპირიული მოდელის ნაკლოვანებად გვევლინება ჰეტეროსკედასტურობა. ნარჩენების ჰეტეროსკედასტურობაზე შემოწმებისას გლეიჯერის ტესტის ერთეულოვანი ჰიპოთეზა მიიღება, 95%-იანი ალბათობით, რაც გულისხმობს ჰეტეროსკედასტურობის არსებობას. შესაბამისად ნარჩენობითი წევრების ვარიაცია არის არის მუდმივი.
ცხრილი6: ცვეთის ნორმის მეორე მიდგომის შემთხვევაში (23) მოდელის ნარჩენობით წევრებში ჰეტეროსკედასტურობის არსებობის შემოწმება გლეიჯერის ტესტის მიხედვით
|
Heteroskedasticity Test: Glejser |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
F-statistic |
3.202538 |
Prob. F(3,41) |
0.0330 |
|
|
Obs*R-squared |
8.543036 |
Prob. Chi-Square(3) |
0.0360 |
|
|
Scaled explained SS |
6.906564 |
Prob. Chi-Square(3) |
0.0749 |
|
|
|
|
|
|
|
|
|
|
|
|
|
ემპირიულ მოდელში ყველა ცვლადი კოეფიციენტების შესახებ მიიღება ერთეულოვანი ჰიპოთეზა სტატისტიკურად ვარგისობის შესახებ, გარდა ცვეთის ნორმისა [2, ანანიაშვილი, გვ. 109-129]. მოდელის აღნიშნული ნაკლოვანებების გათვალისწინებით სასურველია გამოვიყენოთ ცვეთის ნორმის მნიშვნელობის შესახებ პირველი მიდგომა.
თუ (23) მოდელის შეფასებისას ცვეთის ნორმის შესახებ გამოვიყენებთ პირველ მიდგომას, რაც გულისხმობს რომ მისი მნიშვნელობა წარმოადგენს 0.057-ს, მაშინ მივიღებთ:
ცხრილი7: ცვეთის ნორმის პირველი მიდგომის შემთხვევაში უმცირეს კვადრატთა მეთოდით მიღებული (23) მოდელის შეფასებები
|
Dependent Variable: D_LN_I_K_F |
|
|||
|
Method: Least Squares |
|
|
||
|
Date: 06/09/18 Time: 13:08 |
|
|
||
|
Sample (adjusted): 2003Q3 2016Q4 |
|
|||
|
Included observations: 45 after adjustments |
|
|||
|
Convergence achieved after 7 iterations |
|
|||
|
D_LN_I_K_F=1/C(1)* LN_GDP_F+(1-C(1))/C(1)*LN_LP_F+0.057+C(2) |
||||
|
*WAR |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
|
|
|
|
|
|
|
|
|
|
|
|
C(1) |
0.566049 |
0.051367 |
11.01977 |
0.0000 |
|
C(2) |
-1.028846 |
0.201679 |
-5.101393 |
0.0000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
R-squared |
0.794665 |
Mean dependent var |
0.019193 |
|
|
Adjusted R-squared |
0.789890 |
S.D. dependent var |
0.427858 |
|
|
S.E. of regression |
0.196120 |
Akaike info criterion |
-0.376749 |
|
|
Sum squared resid |
1.653919 |
Schwarz criterion |
-0.296453 |
|
|
Log likelihood |
10.47685 |
Hannan-Quinn criter. |
-0.346815 |
|
|
Durbin-Watson stat |
2.141582 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() (24)
(24)
(24) მოდელის სტატისტიკურად ვარგისია, მისი კოეფიციენტების შესახებ მიიღება ერთეულოვანი ჰიპოთეზა სტატისტიკურად საიმედოობის შესახებ [2, ანანიაშვილი, გვ. 109-129]. მოდელს გააჩნია მაღალი ამხსნელობითი უნარი და მისი როგორც დეტერმინაცის ასევე კორექტირებული დეტერმინაციის კოეფიციენტი საკმაოდ მაღალია (0.795; 0.79).
მოდელის ნარჩენობითი წევრები ნორმალ განაწილებას ექვემდებარება, რაც ადასტურებს ზემოთ აღნიშნული ტესტების ვალიდურობას.
გრაფიკი2: (24) მოდელის ნარჩენობითი წევრების განაწილების ჰისტოგრამა
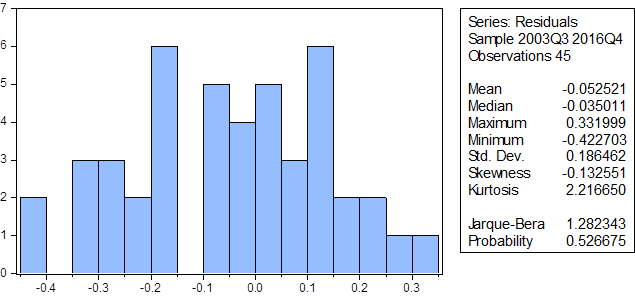
მოდელის ნარჩენობითი წევრებში ავტოკორელაციის შემოწმებისას ბროიშ- გოდფრის ტესტის ნულოვანი ჰიპოთეზა მიიღება 99% საიმედოობით, რაც გულისხმობს რომ ნარჩენობით წევრებში არ შეინიშნება ავტოკორელაცია [16, Breusch, P., 334-355; 22, Godfrey, P. 1293-1301]..
ცხრილი8: (24) მოდელის ნარჩენობითი წევრებში ავტოკორელაციის არსებობის შემოწმება ბროიშ-გოდფრის ტესტის მიხედვით
|
Breusch-Godfrey Serial Correlation LM Test: |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
F-statistic |
1.539773 |
Prob. F(2,41) |
0.2266 |
|
|
Obs*R-squared |
0.000000 |
Prob. Chi-Square(2) |
1.0000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(24) მოდელის ნარჩენობით წევრებში მიიღება გლეიჯერის ტესტის ნულოვანი ჰიპოთეზა ჰომოსკედასტურობის შესახებ 90%-იანი საიმედოობით [21, Glejser..., P. 316-323].
ცხრილი9: (24) მოდელის ნარჩენობითი წევრებში ჰეტეროსკედასტურობის არსებობის შემოწმება გლეიჯერის ტესტის მიხედვით
|
Heteroskedasticity Test: Glejser |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
F-statistic |
2.571338 |
Prob. F(3,41) |
0.0672 |
|
|
Obs*R-squared |
7.125888 |
Prob. Chi-Square(3) |
0.0680 |
|
|
Scaled explained SS |
6.274609 |
Prob. Chi-Square(3) |
0.0990 |
|
|
|
|
|
|
|
|
|
|
|
|
|
საქართველოს ეკონომიკის მაგალითზე (23) მოდელის ემპირიული რეალიზაციით დგინდება, რომ მოდელი სტატისტიკურად ვარგისია [2, ანანიაშვილი, გვ. 109-129]..
მთლიანი ინვესტიციების და ძირითადი კაპიტალის წინა მნიშვნელობის
თანაფარდობასთან ზრდად დამოკიდებულებაშია მშპ-ს მიმდინარე და წინა მნიშვნელობის თანაფრდობა, ხოლო კლებად დამოკიდებულებაშია დასაქმებულთა მიმდინარე პერიოდის თანაფარდობა მის წინა პერიოდის მნიშვნელობასთან. ამასთან ასევე კლებად დამოკიდებულებაშია ომის ფაქტორი საშედეგო ცვლადთან, რაც ლოგიკური შედეგია. ძირითადი კაპიტალის ცვეთის ნორმის მნიშვნელობა, რომელიც გამოთვლილია ინვესტიციების აქსელერატორის მოდელის მეშვეობით წარმოადგენს კარგ შეფასებას, ვინაიდან დამატებითი თავისუფალი წევრის ჩართვით მოდელში თუ მოდელიდან აღნიშნული მნიშვნელობის ამოღებით და ხელახალი შეფასებით მიიღება სტატისტიკურად არამნიშვნელოვანი შედეგები.
ინვესტიციების ემპირიული მოდელის დეტერმინაციის და კორექტირებულ დეტერმინაციის კოეფიციენტები მიგვითითებს, რომ მოდელს აკლია სტატისტიკურად მნიშვნელოვანი სხვა ფაქტორული ცვლადი, რაც ლოგიკურ შედეგს წარმოადგენს. მოდელის ემპირიული რეალიზაციის წინ აღინიშნა, რომ საქართველოს მაგალითზე არ გაგვაჩნდა ინფორმაცია ტექნოლოგიური პროგრესის ცვლადის შესახებ და მოხდა მოდელის ემპირიული შემოწმება აღნიშნული ცვლადის გარეშე. შეიძლება ითქვას, რომ სწორედ აღნიშნულმა ცვლადმა ჰპოვა ასახვა დეტერმინაციის და კორექტირებული დეტერმინაციის კოეფიციენტებში.
აღნიშნული შედეგები მიუთითებს თეორიული მოდელის (22) კორექტულობაზე, რაც გულისხმობს, რომ ქვეყნის ეკონომიკა ყოველ პერიოდში მიისწრაფის მის ბუნებრივ დონემდე. ბუნებრივი დონე დროის ყოველ ტაქტში განიცდის ცვლილებას ტექნოლოგიური პროგრესის მეშვეობით, რაც გულისხმობს, რომ ქვეყნის ეკონომიკის შესაძლებლობის ზედა საზღვარი განიცდის ცვლილებას.
მნიშვნელოვანია აღინიშნოს, რომ მიღებული შედეგები ეფუძნება რამდენიმე მნიშვნელოვან დაშვებას, კერძოდ:
- ქვეყნის ეკონომიკის მასშტაბის მუდმივ უკუგებას;
- კაპიტალისა და შრომის კლებადი უკუგების შესახებ;
- დროის ყოველ პერიოდში ეკონომიკა მიისწრაფის მის ბუნებრივ დონემდე;
- დროის ყოველ ტაქტში ტექნოლოგიური ცვლილებების გამო იცვლება მშპ-ს ბუნებრივი დონე და იგი განისაზღვრება, როგორც წინა დროითი ტაქტის ბუნებრივი დონის მოცულობის ნამრავლით მიმდინარე პერიოდისა და წინა პერიოდის ტექნოლოგიური პროგრესის ცვლადების ფარდობაზე.
დასკვნა
სტატიაში წარმოდგენილია კობ-დუგლასის, ეკონომიკის ბუნებრივი დონისა და ინვესტიციების თეორიის სინთეზისგან მიღებული ინვესტიციების მოდელი.
![]()
ეკონომიკის ბუნებრივი დონიდან გადახრის დამახასიათებელი ინვესტიციების მულტიპლიკატიური მოდელით დადგენილია მთლიან ინვესტიციების რაოდენობის კავშირი, წინა პერიოდის კაპიტალის მოცულობასთან, მშპ-ს, დასაქმებულთა რაოდენობის, ფარდობითი ტექნოლოგიური ცვლადის მიმდინარე და ლაგირებულ მნიშვნელობებთან და კაპიტალის ცვეთის ნორმასთან. აღნიშნული ინვესტიციების მოდელი ეფუძნება დაშვებებს: 1) ქვეყნის ეკონომიკის მასშტაბის მუდმივ უკუგებას; 2) კაპიტალისა და შრომის კლებადი უკუგების შესახებ; 3) დროის ყოველ პერიოდში ეკონომიკა მიისწრაფის მის ბუნებრივ დონემდე; 4) დროის ყოველ ტაქტში ტექნოლოგიური ცვლილებების გამო იცვლება მშპ-ს ბუნებრივი დონე და იგი განისაზღვრება, როგორც წინა დროითი ტაქტის ბუნებრივი დონის მოცულობის ნამრავლით მიმდინარე პერიოდისა და წინა პერიოდის ტექნოლოგიური პროგრესის ცვლადების ფარდობაზე.
საქართველოს ეკონომიკის მაგალითზე ეკონომიკის ბუნებრივი დონიდან გადახრის დამახასიათებელი ინვესტიციების მულტიპლიკატიური მოდელის ემპირიული რეალიზაციით დგინდება, რომ მოდელი სტატისტიკურად ვარგისია. მთლიანი ინვესტიციებისა და ძირითადი კაპიტალის წინა მნიშვნელობის თანაფარდობასთან ზრდად დამოკიდებულებაშია მშპ-ს მიმდინარე და წინა მნიშვნელობის თანაფრდობა, ხოლო კლებად დამოკიდებულებაშია დასაქმებულთა მიმდინარე პერიოდის თანაფარდობა მის წინა პერიოდის მნიშვნელობასთან. ამასთან, ასევე კლებად დამოკიდებულებაშია ომის ფაქტორი საშედეგო ცვლადთან, რაც ლოგიკური შედეგია. ძირითადი კაპიტალის ცვეთის ნორმის მნიშვნელობა, რომელიც გამოთვლილია ინვესტიციების აქსელერატორის მოდელის მეშვეობით, წარმოადგენს კარგ შეფასებას, ვინაიდან დამატებითი თავისუფალი წევრის ჩართვით მოდელში თუ მოდელიდან აღნიშნული მნიშვნელობის ამოღებით და ხელახალი შეფასებით მიიღება სტატისტიკურად არამნიშვნელოვანი შედეგები.
ინვესტიციების ემპირიული მოდელის დეტერმინაციის და კორექტირებულ დეტერმინაციის კოეფიციენტები მიგვითითებს, რომ მოდელს აკლია სტატისტიკურად მნიშვნელოვანი სხვა ფაქტორული ცვლადი, რაც ლოგიკურ შედეგს წარმოადგენს. მოდელის ემპირიული რეალიზაციის წინ აღინიშნა, რომ საქართველოს მაგალითზე არ გაგვაჩნდა ინფორმაცია ტექნოლოგიური პროგრესის ცვლადის შესახებ და მოხდა მოდელის ემპირიული შემოწმება აღნიშნული ცვლადის გარეშე. შეიძლება ითქვას, რომ სწორედ აღნიშნულმა ცვლადმა ჰპოვა ასახვა დეტერმინაციის და კორექტირებული დეტერმინაციის კოეფიციენტებში.
აღნიშნული შედეგები მიუთითებს თეორიული მოდელის კორექტულობაზე, რაც გულისხმობს, რომ ქვეყნის ეკონომიკა ყოველ პერიოდში მიისწრაფის მის ბუნებრივ დონემდე. ბუნებრივი დონე დროის ყოველ ტაქტში განიცდის ცვლილებას ტექნოლოგიური პროგრესის მეშვეობით, რაც გულისხმობს, რომ ქვეყნის ეკონომიკის შესაძლებლობის ზედა საზღვარი განიცდის ცვლილებას
გამოყენებული ლიტერატურა
- ანანიაშვილი, ი. დროითი მწკრივების ანალიზი. თბილისის უნივერსიტეტის გამომცემლობა, თბილისი (2014).
- ანანიაშვილი, ი. ეკონომეტრიკა. გამომცემლობა მერიდიანი. თბილისი (2010).
- ანანიაშვილი, ი. სალექციო კურსი. მაკრომოდელირება1. თბილისი (2014).
- ბლანშარი, ო. მაკროეკონომიკა. თბილისის უნივესრიტეტის გამომცემლობა, თბილისი (2010).
- გელაშვილი ს., სტატისტიკური პროგნოზირება ეკონომიკასა და ბიზნესში. წიგნი I. გამომცემლობა ,,მერიდიანი”. თბილისი (2017).
- გელაშვილი, ს. სტატისტიკური ინერციულობა და R-პროგრამის გამოყენების შესაძლებლობა ეკონომიკურ პროგნოზირებაში. საერთაშორისო სამეცნიერო შრომების კრებული: თანამედროვე ინფორმაციული ტექნოლოგიები გლობალიზაციის პირობებში. თბილისის უნივერსიტეტის გამომცემლობა, თბილისი (2015).
- გელაშვილი, ს. სტატისტიკური პროგნოზირება თანამედროვე ბიზნესში. მონოგრაფია, გამომცემლობა მერიდიანი. თბილისი (2012).
- მიქელაძე, გ. ინვესტიციების აქსელერატორის და ტობინის მოდელი (საქართველოსმაგალითზე), საერთაშორისო სამეცნიერო-ანალიტიკური ჟურნალი „ეკონომისტი“, № 4 (2017).
- მიქელაძე, გ. ინვესტიციების ეკონომეტრიკულ-სტატისტიკური მოდელები და მათი ემპირიული რეალიზაციის შესაძლებლობები საქართველოში. პროფესორ გიორგი წერეთლის დაბადებიდან 65-ე წლისთავისადმი მიძღვნილი საერთაშორისო სამეცნიერო კონფერენციის მასალათა კრებული „ეკონომიკური განვითარების სტრუქტურული და ინოვაციური პრობლემები“, (2017), გვ 215-220.
- მიქელაძე, გ. ინვესტიციების ფულადი ნაკადების მოდელის ემპირიული რეალიზაცია (საქართველოს მაგალითზე). საერთაშორისო სამეცნიერო ანალიტიკური ჟურნალი „ეკონომისტი“,№ 3 (2017).
- მიქელაძე, გ. ინვესტიციების ნეოკლასიკური მოდელის ემპირიული რეალიზაცია საქართველოს მაგალითზე, ეკონომიკა, № 7-8, 2016 წ., გვ. 50-56, საქართველოს ტექნიკური უნივერსიტეტი, თბილისი (2016).
- მიქელაძე, გ. საქართველოს ძირითადი კაპიტალი და მისი გამოთვლის ალტერნატიული მეთოდები. ჟ. ეკონომიკა №5-6 (2016); გვ. 94-111.
- მიქიაშვილი, ნ., გამოყენებითი ეკონომეტრიკა. სალექციო კურსი. თბილისის უნივერსიტეტის გამომცემლობა. თბილისი (2015).
- თოთლაძე, ლ., ეკონომიკური პროგნოზირების მოდელები და მეთოდები. სალექციო კურსი. თბილისის უნივერსიტეტის გამომცემლობა. თბილისი (2015).
- Берндт Эрнст Р., Практика зконометрики: классика и современность., Юнити-Дана, Москва, Ст 847, 2005.
- Breusch, Trevor S. “Testing for autocorrelation in dynamic linear models”. Australian Economic Papers 17.31 (1978): 334-355.
- Dickey, David A., and Wayne A.Fuller. “Distribution of the estimators for autoregressive time series with a unit root. “Journal of the American statistical association 74.366a (1979): 427-431.
- Diebold, Francis X., and Jose A. Lopez. "8 Forecast evaluation and combination." Handbook of statistics 14 (1996): 241-268.
- Dolado, Juan J., Tim Jenkinson, and Simon Sosvilla-Rivero. “Cointegration and unit roots.” Journal of economic surveys 4.3 (1990): 249-273.
- Elgar Edward., Modern macroeconomics., 807 pg., UK., 2005.
- Glejser, Herbert. "A new test for heteroskedasticity." Journal of the American Statistical Association 64.325 (1969): 316-323.
- Godfrey, Leslie G. “Testing against general autoregressive and moving average error models when the regressors include lagged dependent variables.” Econometrica: Journal of the Econometric Society (1978): 1293-1301.
- Jorgenson, Dale W. "Capital theory and investment behavior." The American Economic Review 53, no. 2 (1963): 247-259.
- Kopcke, Richard W., Forecasting Investment Spending: The Performance os statistical Models. New England Economic Review, Boston. Mass.: Federal Reserve Bank of Boston. November/December., 13-32., 1982.
- Kopcke, Richard W., The Behavior of Investment Spending during the Recession and Recovery. New England Economic Review, Boston. Mass.: Federal Reserve Bank of Boston. November/December .,5-4., 1977.
- Kopcke, Richard W.,The Determinants of Investment Spending New England Economic Review, Boston. Mass.: Federal Reserve Bank of Boston. July/August .,19-35., 1985.
- Muchiashvili, M., Effects of FDI on the economic growth of Georgia., Journal Economist no 2 (2012): 33-36.
- Winfrey,Robert., Statistical Analyses of Industrial Property Retirement, Ames, lowa: lowa Engineering Experiment Station, Bulletin 123, December., 11.,1935.
- Wooldridge, Jeffrey M. Introductory econometrics: A modern approach. Nelson Education, 2015.
- Zellner, Arnold, Jan Kmenta, and Jacques Dreze. "Specification and estimation of Cobb-Douglas production function models."Econometrica:Journal of the Econometric Society (1966):784-795.
- საქართველოს სტატისტიკის ეროვნული სამსახური, მშპ-ს მოცულობა, ხელმისაწვდომია ელ-მისამართზე: http://geostat.ge/?action=page&p_id=118&lang=geo, ვებ-გვერდი ბოლოს ნანახია 20.06.2018.
- საქართველოს სტატისტიკის ეროვნული სამსახური, საწარმოთა ბრუნვა, ხელმისაწვდომია ელ-მისამართზე: http://geostat.ge/?action=page&p_id=211&lang=geo, ვებ-გვერდი ბოლოს ნანახია 20.06.2018.
- საქართველოს სტატისტიკის ეროვნული სამსახური, მთლიანი ინვესტიციების რაოდენობა. ხელმისაწვდომია ელ-მისამართზე: http://geostat.ge/?action=page&p_id=118&lang=geo, ვებ-გვერდი ბოლოს ნანახია 20.06.2018.
- საქართველოს სტატისტიკის ეროვნული სამსახური, შინამეურნეობების ინტეგრირებული, შემოსავლებისა და ხარჯების ელექტრონულ მონაცემთა ბაზა ხელმისაწვდომია ელ-მის.: http://geostat.ge/?action=meurneoba&mpid=1&lang=geo, ვებ-გვერდი ბოლოს ნანახია 20.06.2018.





